Project 3: From CA to LBM

---

Goal of Project 3 [<<] [<] [>]

In this project, we hope you can use all knowledge about computer architecture that your have learned in this course to optimize lattice Boltzmann methods (LBM). The figure below is an example of LBM.

From CA to lattice Boltzmann methods (LBM) [<<] [<] [>]

A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are composed of a group of cells (or grids) with a set of rules. Each cell has a certain state (such as alive or dead). After assigning initial states and evolution rules, the state of each cell at the next moment is determined by the state of the cell in the previous moment and the state of the surrounding cells (neighbors). The most well-known cellular automaton is undoubtedly the Game of Life.

The concept of cellular automata has given rise to many applications. In the field of fluid mechanics, the earliest and most prominent application was the Lattice Gas Automaton (LGA). In LGA, the particles move across a lattice of cells and collide with each other according to certain rules. In the 2-dimensional FHP Model (a classic LGA model) each lattice node is connected to its neighbors by 6 lattice velocities on a triangular lattice; there can be either 0 or 1 particle at a lattice node moving with a given lattice velocity. After a time interval, each particle will move to the neighboring node in its direction; this process is called the propagation or streaming step. When more than one particle arrives at the same node from different directions, they collide and change their velocities according to a set of collision rules. Streaming steps and collision steps alternate. Suitable collision rules should conserve the particle number (mass), momentum, and energy before and after the collision.

Later, people replaced the evolution equation of LGA with the Boltzmann transport equation, which converts the particle's state from discrete to a distribution function of the Boltzmann equation, and replaced Boolean operations with real number operations. In the lattice Boltzmann methods (LBM), every cell has their particles distribution on the different speed direction. As with LGA, each time step requires two important steps: collision steps and streaming steps.

In collision steps, one method is to use Bhatnagar-Gross-Krook (BGK) relaxation term to discretize Boltzmann equation. This lattice BGK (LBGK) model makes simulations more efficient and allows flexibility of the transport coefficients. In the following equation, f^{eq} is the distribution of particles at each velocity of the current lattice in the equilibrium state.

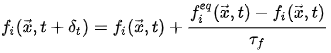
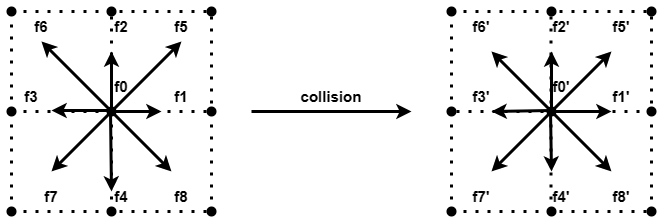
In streaming steps, the particles flow in their corresponding speed direction to the next cell. As shown below, where e_{i} is the speed direction of the particles distribution.

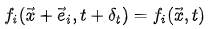
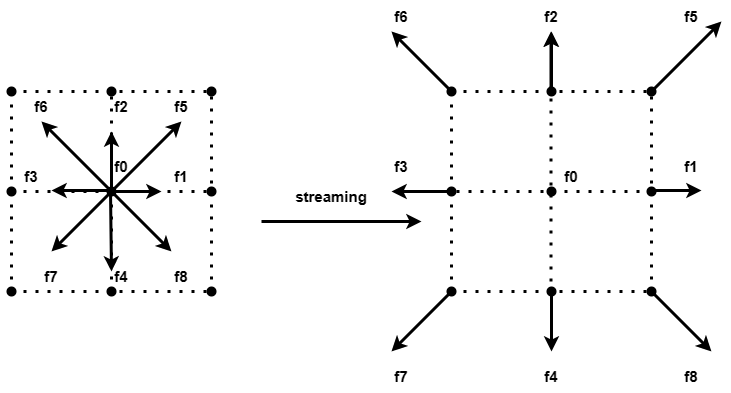
Here we are using the d2q9 model, d2 means a two-dimensional grid, and q9 means there are 9 velocity directions in each cell. That is, each cell has 9 velocity components. There is a corresponding particle distribution at each velocity. As shown in the figure below, the speed 0 represents the speed that remains motionless in the current cell, and the other 8 speeds point to the surrounding 8 neighbor cells. During the streaming step, these particles stream into the cells corresponding to their speeds.

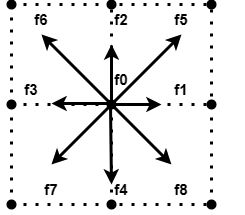
In addition to the above two most important steps, we also need to consider collisions with obstacles and the handling of boundary conditions.

Collisions with obstacles can simply be thought of as non-relative sliding, i.e. particles bounce in exactly the opposite direction to the direction of incidence.

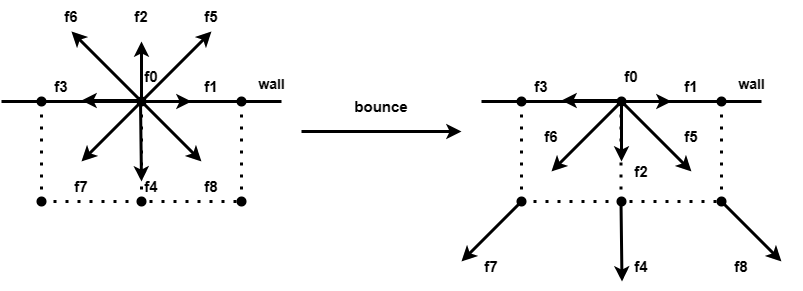
The handling of boundaries are a little more complicated, and here we treat the upper and lower boundaries as the same fully bounced boundaries as the obstacle. The left boundary is a boundary of constant velocity and the right boundary is a boundary of a first-order approximation to the cells on its left, so as to simulate the effect of the fluid entering the simulation area from the left and leaving on the right.

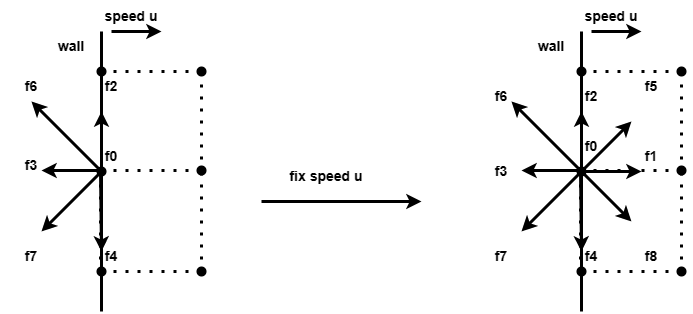
At this point we have completed a brief introduction to LBM, if you still have doubts, you can check the related information or read the code we provide.

Getting started

Make sure you read through the entire specification before starting the project.

You will be using gitlab to collaborate with your group partner. Autolab will use the files from gitlab. Make sure that you have access to gitlab. In the group CS110_23s_Projects you should have access to your project 3 project. Also, in the group CS110_23s, you should have access to the p3_framework.

Obtain your files

1. Clone your p3 repository from GitLab.
2. In the repository add a remote repo that contains the framework files: git remote add framework https://autolab.sist.shanghaitech.edu.cn/gitlab/cs110_23s/p3_framework.git
3. Go and fetch the files: git fetch framework
4. Now merge those files with your master branch: git merge framework/master
5. The rest of the git commands work as usual.

Files

The framework contains the following files and directories:

• data/ - A folder containing test parameters and reference results.
• scripts/ - A folder that contains scripts for visualizing results and correctness tests.
• calc.c - A file contains calculation functions that are not used for the main iterative process.
• d2q9_bgk.c - A file that contain the most important iterations of the process, the files that you should pay the most attention to.
• main.c - A file contains the main function that describes the entire flow of the program.
• types.h - The file contains global type definitions.
• utils.c - A file contains some utility functions used for initialization, destruction, and output files.
• Makefile - You can change the contents of the Makefile, including compiler option, as you like, but you need to ensure that the name of the generated executable, as well as the input format accepted by the file and the format of the output file, remain unchanged. We will use make all to generate the executable.

Run program

You can compile the program with Makefile as follows

• make all - Compile program into a file lbm
• make visual - Run LBM with simple configuration, output with an animated GIF.
• make evaluate - Run LBM with configuration for evaluation.
• make plot - Plot a figure for final state.

You can also run the program by passing some arguments into it as follow:

lbm <paramfile> <obstaclefile> [output_directory]

Optimization Techniques

You can find many obvious optimizations in the implementation we provide, with what you have learnt in Computer Architecture. We are listing some of the possible approaches below:

Algorithm

You are not allowed to optimize the naive algorithm we give though, as this is not the focus of Computer Architecture. You will receive no point if we find you do that.

Compiler

There are some optimization flags that can be turned on in GCC. The available flags for x86 ISA from GCC is listed here. You can try to optimize with different compiler options, but you need to be clear about what the options do. You will be asked in a later check in lab about why you have chosen this compiler option.

Multithreading

The first and the easiest approach is to use multithreading to optimize this algorithm, with either pthread or openmp.

SIMD instructions

Part of the algorithm is also a good candidate for SIMD instructions. You can use SIMD in a variety of ways, such as you can implement SIMD in different dimensions by changing the data structure. However, please note that you need to ensure that the content of the output file is the same as the original.

Cache

Optimizing for cache is probably the hardest part of this project. First of all, please complete the above two optimizations to shorten the calculation time. Then consider the access behavior of the whole program to memory, think about whether this form of access is cache-friendly and how to make the program more cache-friendly, you need to pay attention to the dependencies between data, and find a suitable way to improve the utilization of the cache without breaking the dependencies between the data. Some methods of improving cache access performance may have some damage to parallelism. You need to find a way to balance parallelism with cache access efficiency. It is helpful to consider the specific cache capacity.

For your reference, in the case of multithreading and SIMD, if you make full use of the cache, cache misses can be reduced by at least 60%, and performance can be improved by at least 40%.

Grading Policy

Your grade will be divided into two parts:

1. We will first run your code on test cases on Autolab. If you program produces the correct result and satisfy our time requirement, you receive 40% points. (For your reference, if you only add some lines of #pragma omp parallel for, the running time will be between 1 minute and 2 minutes.)
2. After the due, we will test your code on final test server. Your grade on this part depends on the execution time of your code. All groups run slower than 1 minute but faster than 2 minutes get 20% points and the fastest 15 groups receive 60% points. The execution time of 15th group is 60% line and 1 minute is 20% line. The grades for the remaining groups are linearly distributed according to their execution time.

There are also some minimum requirements you should meet to get points:

• Your code should not crash on either stage, or you will receive no point from both stages.
• Your submission must contain meaningful use of OpenMP(or pthread) and Intel SIMD intrinsics. Otherwise, you will receive no point from both stages. This check will be done manually after the deadline so there will be no feedback on this from Autolab.

Submission

When your project is done, please submit all the files including the framework to your remote GitLab repo by running the following commands.

$ git commit -a
$ git push origin master:master

How to Autolab

Similar to previous projects, upload your autolab.txt to Autolab to submit your project.

Submission Time Announcement

The last time of your submission to the git repo will count towards your submission time - also with respect to slip days. So do not commit to this git after the due date, unless you want to use slip days or are OK with getting fewer points.

Collaborative Coding and Frequent Pushing

You have to work at this project as a team. We invite you to use all of the features of gitlab for your project, for example branches, issues, wiki, milestones, etc.

We require you to push very frequently to gitlab. In your commits we want to see how the code evolved. We do NOT want to see the working code suddenly appear - this will make us suspicious.

We also require that all group members do substantial contributions to the project. This also means that one group member should not finish the project all by himself, but distribute the work among all group members!

At the end of Project 3 we will interview all group members and discuss their contributions, to see if we need to modify the score for certain group members.

Test Cases

There will be two tests on AutoLab. They have the following dimension parameters.

nx: 4096 ny: 512 iters: 1000

nx: 1024 ny: 128 iters: 10000

The final performance test has only one type parameters.

nx: 4096 ny: 512 iters: 5000

Every test includes a correctness check.

Server Configurations

Autolab Server (Just for your reference):

• CPUs: 2 * Intel Xeon E5-2690 v4 2.6 GHz Details here
• Memory: 256 GiB 4-channel DDR4 (shared by all student tasks)
• 4 cores are allowed for each grading job

Toast Lab Server (Used for final speed test):

• CPU: Intel Xeon E5-2690 v4 2.6 GHz, 14 cores (28 threads) Details here

  • L1 i-cache 32 KiB (per core)
  • L1 d-cache 32 KiB (per core)
  • L2 cache 3.5 MiB (unified)
  • L3 cache 35 MiB (unified)

• Memory: 120 GiB

More about the final speed test

The final test server in fact has two cpus that uses the NUMA architecture which is commonly used in modern servers. In the final test we will use numactl to run the program in a NUMA node. This is to avoid the impact of NUMA's memory arrangement on openmp. If you're interested, you can find out what numa is and why it has an effect on openmp. But we're not asking too much here, you can simply think of it as having only one CPU with 14 cores, as the same as the server configurations listed above.